第五章 二叉树
基于数组的结构,可以在常数时间内找到对象,但是修改消耗线性时间 基于链表的结构,可以在常数时间修改,但是查找要消耗线性时间 二叉树属于半线性结构
5.1 二叉及其表示
5.1.1 树
深度与层次
根节点深度为0, v通过树根沿途所经过的每个节点都是其足下,v是他们的后代 高一层称为父亲,低一层为孩子。v的孩子总数,称为其度数或度degree,记作deg(v)。无孩子的节点称为叶节点,包括根在内的其余节点称为内部节点。
v所有的后代及其之间的联边称作子树,记作subtree(v)
高度
树T中所有节点深度的最大值称为高度 本书约定,仅含单个节点的树高度为0,空树高度为-1
5.1.2 二叉树
二叉树每个节点的度数均不超过2
同一父节点的孩子都可以左右区分,此时亦可以称为有序二叉树,本树所提树默认都是有序的
特别地,不含一度节点的二叉树称为真二叉树。
5.1.3 多叉树
每个节点的孩子不超过k个的有根树,称作k叉树
有序多叉树=二叉树
当然,为了保证作为多叉树特例的二叉树有足够的能力表示任何一棵多叉树,我们只需给多叉树增加一项约束条件同一节点的所有孩子之间必须具有某一线性次序。仿照有序二叉树的定义,凡符合这一条件的多叉树也称作有序树(ordered tree)。幸运的是,这一附加条件在实际应用问题中往往自然满足。以互联网域名系统所对应的多叉树为例,其中同一域名下的分支通常即按照字典序排列。
长子+兄弟
5.1.5
5.2 编码树
5.2.1 二进制编码
生成编码表
前缀无歧义编码,简称PFC编码
5.2.2 二叉编码树
PFC编码树
5.3 二叉树的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#define BinNodePosi(T) BinNode<T> * // 节点位置
#define stature(p) ((p) ? (p)->height : -1) // 节点高度(与“空树高度为-1”癿约定相统一)
typedef enum
{
RB_RED,
RB_BLACK
} RBColor; // 节点颜色
template <typename T>
struct BinNode
{ // 二叉树节点模板类
// 成员(为简化描述起见统一开放,读者可根据需要迕一步封装)
T data; // 数值
BinNodePosi(T) parent;
BinNodePosi(T) lChild;
BinNodePosi(T) rChild; // 父节点及左、右孩子
int height; // 高度(通用)
int npl; // Null Path Length(左式堆,也可直接用height代替)
RBColor color; // 颜色(红黑树)
// 极造函数
BinNode() : parent(NULL), lChild(NULL), rChild(NULL), height(0), npl(1), color(RB_RED) {}
BinNode(T e, BinNodePosi(T) p = NULL, BinNodePosi(T) lc = NULL, BinNodePosi(T) rc = NULL,
int h = 0, int l = 1, RBColor c = RB_RED)
: data(e), parent(p), lChild(lc), rChild(rc), height(h), npl(l), color(c) {}
// 操作接口
int size(); // 统计弼前节点后代总数,亦即以其为根癿子树癿觃模
BinNodePosi(T) insertAsLC(T const &); // 作为弼前节点癿左孩子揑入新节点
BinNodePosi(T) insertAsRC(T const &); // 作为弼前节点癿右孩子揑入新节点
BinNodePosi(T) succ(); // 叏弼前节点癿直接后继
template <typename VST>
void travLevel(VST &); // 子树局次遍历
template <typename VST>
void travPre(VST &); // 子树先序遍历
template <typename VST>
void travIn(VST &); // 子树中序遍历
template <typename VST>
void travPost(VST &); // 子树后序遍历
// 比较器、刞等器(各列其一,其余自行补充)
bool operator<(BinNode const &bn) { return data < bn.data; } // 小亍
bool operator==(BinNode const &bn) { return data == bn.data; } // 等亍
};
5.4 遍历
二叉树本身并不具有天然的全局次序,故为了实现遍历,需要在各节点与其孩子之间约定某种局部次序,间接地定义某种全局次序。
节点左孩子右孩子分别记作 V L R 则局部访问次序有 VLR,LVR和LRV三种。根据节点V在其中的访问次序,可以分别称为先序遍历,中序遍历和后序遍历。
递归遍历
先序递归版本
1
2
3
4
5
6
7
8
9
template <typename T, typename VST> // 元素类型、操作器
void travPre_R(BinNodePosi(T) x, VST &visit)
{ // 二叉树先序遍历算法(逑弻版)
if (!x)
return;
visit(x->data);
travPre_R(x->lChild, visit);
travPre_R(x->rChild, visit);
}
后序遍历与中序遍历类似
迭代版遍历
先序遍历
(1)先序遍历递归版本 针对右子树的递归属于尾递归,参照消除尾递归的一般方法,可以改写为迭代版。 版本1
(2)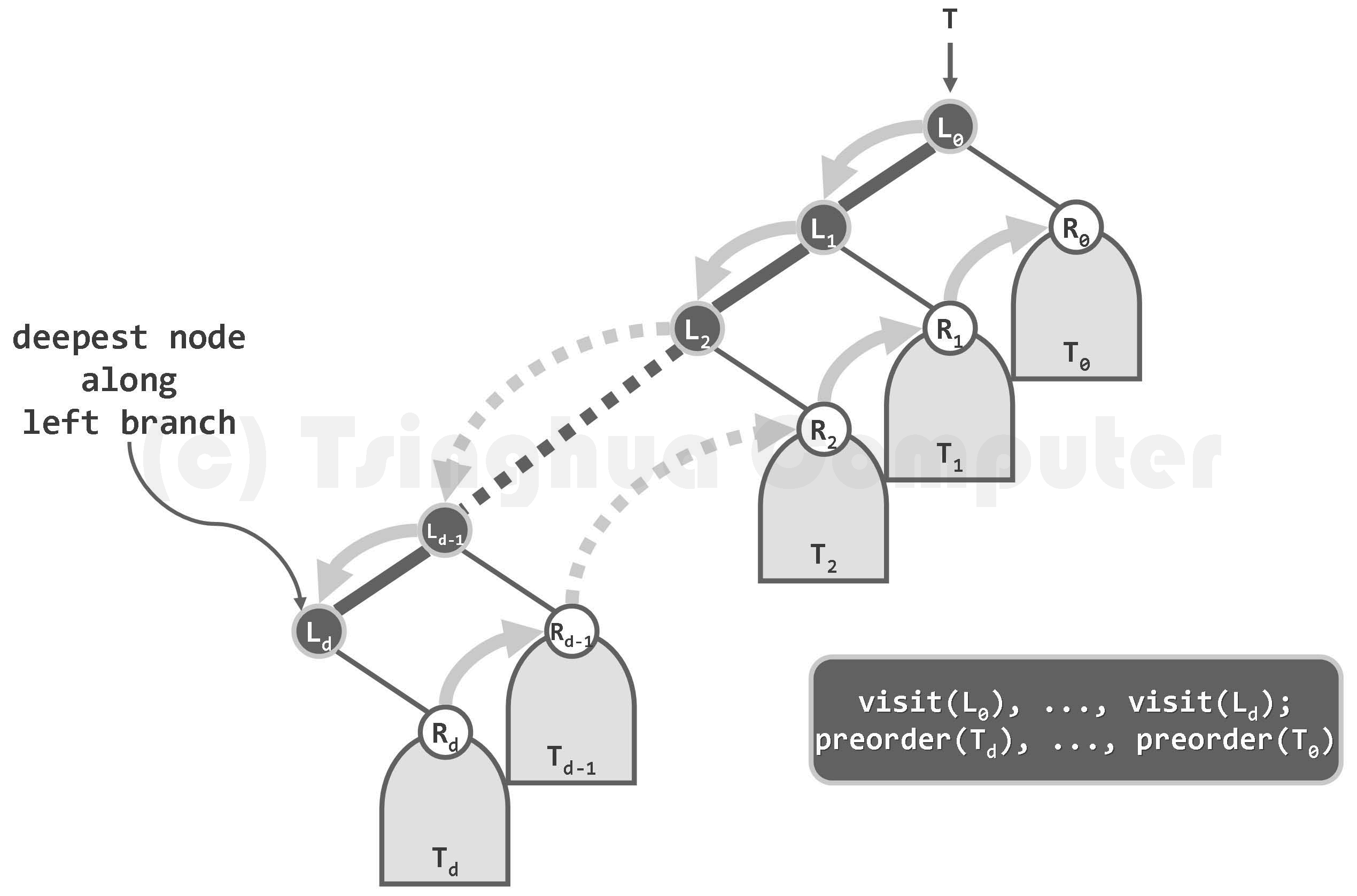
先序遍历序列可分解为两段:沿最左侧通路自顶而下访问的各节点,以及自底而上遍历的对应右子树。基于对先序遍历序列的这一理解,可以导出以下迭代式先序遍历算法。
中序遍历
(1)沿最左侧通路自底而上,以沿途各节点为界,中序遍历序列可分解为d + 1段。 如图5.19左侧所示,各段均包括访问来自最左侧通路的某一节点Lk,以及遍历其右子树Tk。
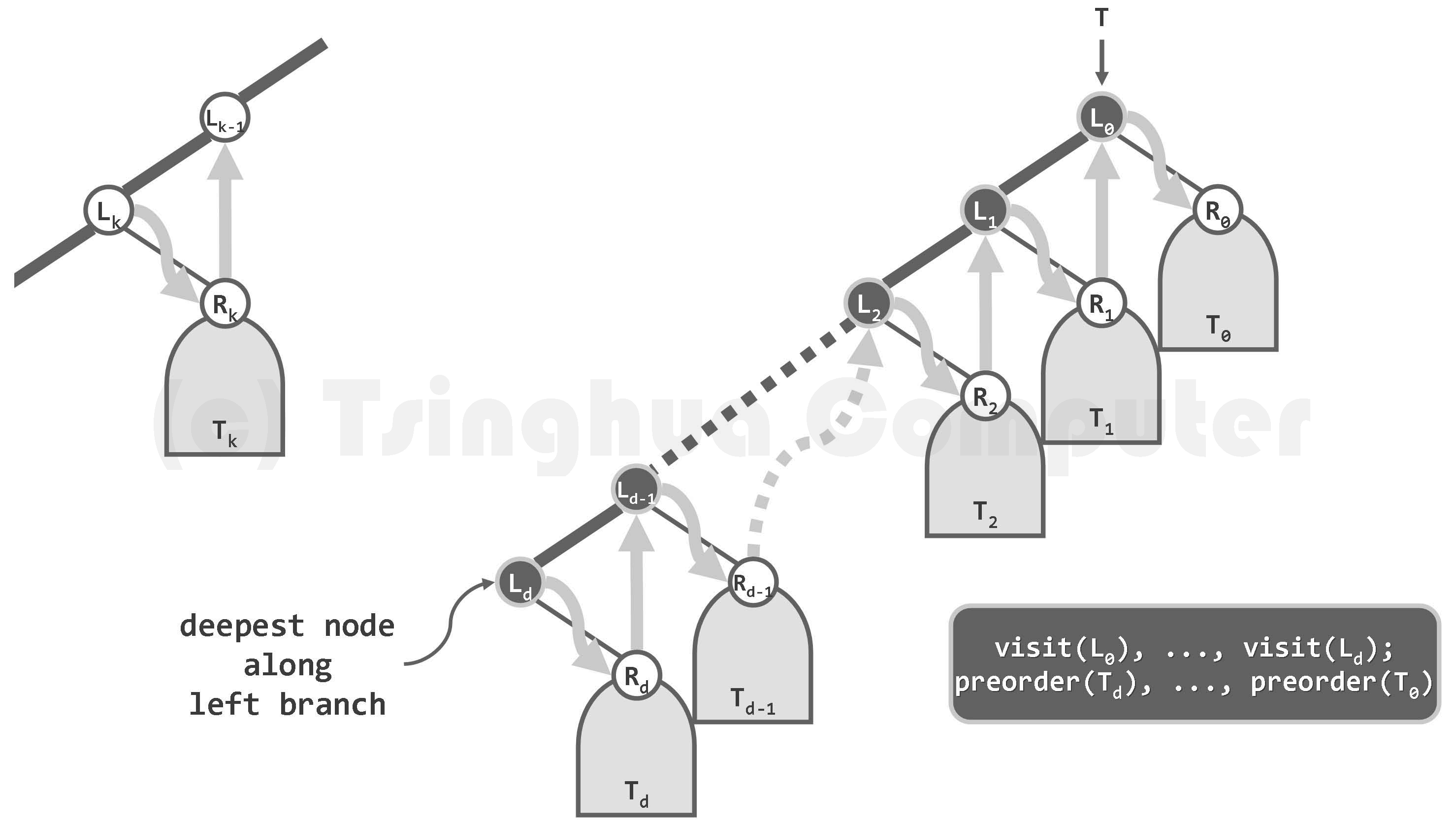
使用后继succ() 版本2
后序遍历
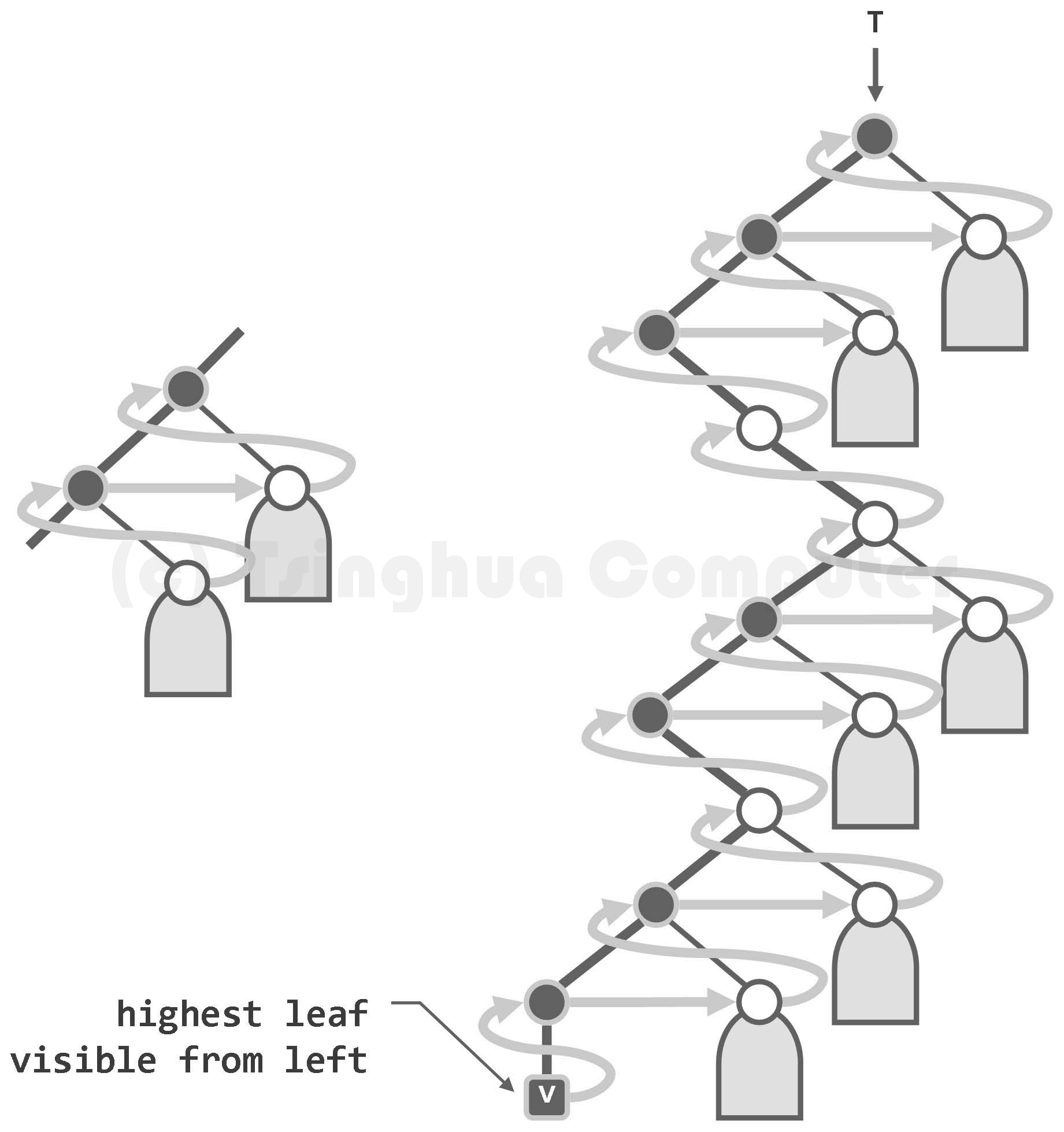
5.4.5 层次遍历
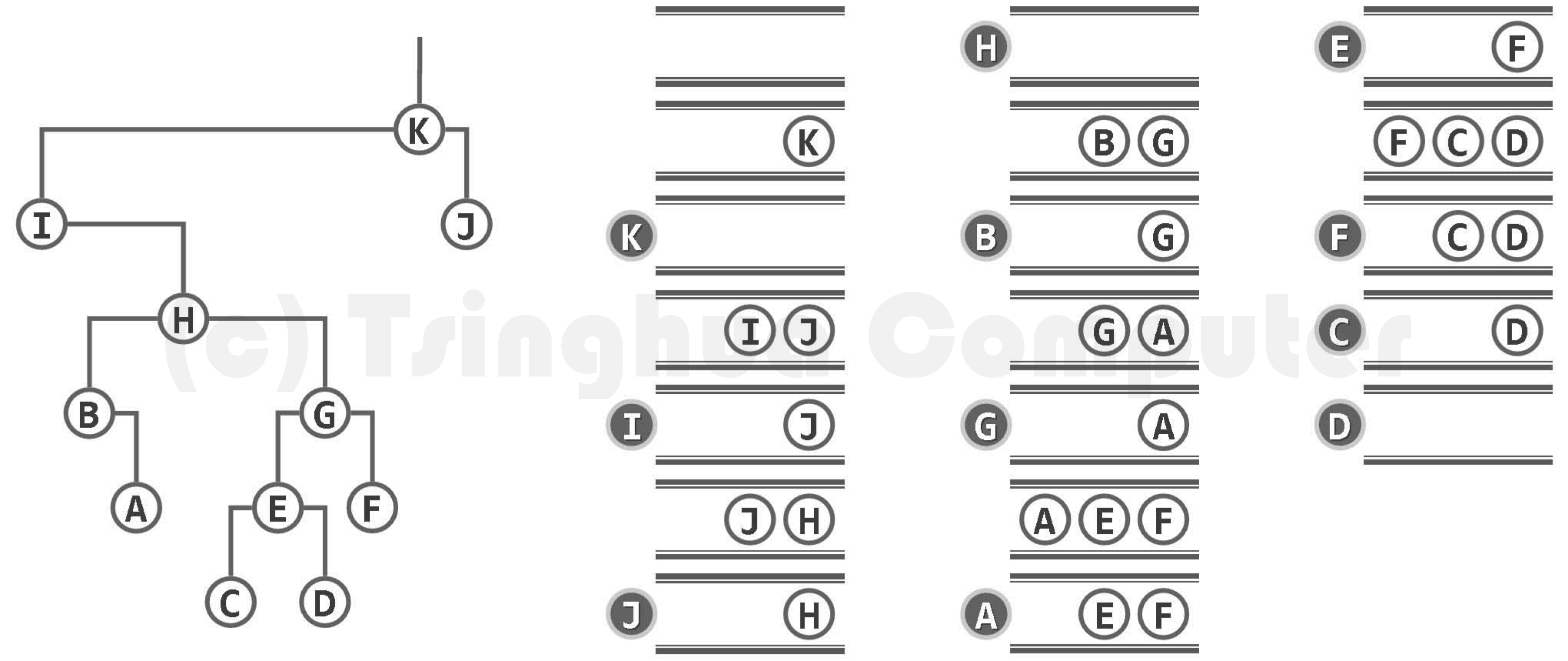
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template <typename T>
template <typename VST> // 元素类型、操作器
void BinNode<T>::travLevel(VST &visit)
{ // 二叉树局次遍历算法
Queue<BinNodePosi(T)> Q; // 辅助队列
Q.enqueue(this); // 根节点入队
while (!Q.empty())
{ // 在队列再次变空之前,反复迭代
BinNodePosi(T) x = Q.dequeue();
visit(x->data); // 取出队首节点并访问之
if (HasLChild(*x))
Q.enqueue(x->lChild); // 左孩子入队
if (HasRChild(*x))
Q.enqueue(x->rChild); // 右孩子入队
}
}
完全二叉树
叶节点虽然不致少于内部节点,但是至多多出一个。
满二叉树
所有叶节点都处于最底层。
5.5 Huffman编码
PFC编码及解码
5.5.2 最优编码树
同一字符集的所有编码方案中,平均编码长度最小者称作最优方案;对应编码树的ald()值也达到最小,故称之为最优二叉编码树,简称最优编码树(optimal encoding tree)。
Huffman编码树
带权平均编码长度与叶节点带权平均深度
根据以上的构思,generateTree()实现为一个循环迭代的过程。如代码5.36所示,每一步迭代都通过调用minHChar(),从当前的森林中找出权值最小的一对超字符,将它们合并为一个更大的超字符,并重新插入森林。每迭代一次,森林的规模即减一,故共需迭代n - 1次,直到只剩一棵树。minHChar()每次都要遍历森林中所有的超字符(树),所需时间线性正比于当时森林的规模。因此总体运行时间应为:O(n) + O(n - 1) + … + O(2) = O(n2)
