首页 Algorithms-DengNo3
文章
取消

Algorithms-DengNo3

发表于 2022/12/29
作者 WaveDragon
15 分钟阅读

第三章 列表

循链接访问

3.1 从向量到列表

3.1.1 从静态到动态

size()和get()等静态操作均可以在常数时间完成。而insert()和remove()等动态操作却需要线性时间。究其原因，在于各个元素物理地址连续—即所谓的静态存储策略

而列表结构未对物理地址做限制，即动态存储策略。

链表linked list即是一种典型的动态存储结构

3.1.2 由秩到位置

3.1.3 列表

列表是具有线性逻辑次序的一组元素构成的集合。 列表是链表结构的一般化推广，其中元素称为节点(node)。与向量一样，在元素之间也可以定义前驱、直接前驱、以及后继和直接后继等关系。

3.2 接口

3.2.1 列表接口

ListNode模板类

1
2
3
4
5
6
7
8
9
10
11
12
13
14

using Rank = int; //秩
template <typename T> struct ListNode;
template <typename T> using ListNodePosi = ListNode<T>*; //列表节点位置
template <typename T> struct ListNode { //列表节点模板类（以双向链表形式实现）
 // 成员
    T data; ListNodePosi<T> pred; ListNodePosi<T> succ; //数值、前驱、后继
 // 构造函数
    ListNode() {} //针对header和trailer的构造
    ListNode ( T e, ListNodePosi<T> p = NULL, ListNodePosi<T> s = NULL )
       : data ( e ), pred ( p ), succ ( s ) {} //默认构造器
 // 操作接口
    ListNodePosi<T> insertAsPred ( T const& e ); //紧靠当前节点之前插入新节点
    ListNodePosi<T> insertAsSucc ( T const& e ); //紧随当前节点之后插入新节点
 };

3.2.2 列表

ADT接口

List模板类

3.3 列表

3.3.1 头尾节点

哨兵节点

3.3.2 默认构造方法

1
2
3
4
5
6
7

template <typename T> void List<T>::init() { //列表初始化，在创建列表对象时统一调用
    header = new ListNode<T>; //创建头哨兵节点
    trailer = new ListNode<T>; //创建尾哨兵节点
    header->succ = trailer; header->pred = NULL;
    trailer->pred = header; trailer->succ = NULL;
    _size = 0; //记录规模
 }

3.3.3 由秩到位置的转换

重载操作符[ ]，提供转换接口
1
2
3
4
5
6

 template <typename T> //重载下标操作符，以通过秩直接访问列表节点（虽方便，效率低，需慎用）
 T& List<T>::operator[] ( Rank r ) const { //assert: 0 <= r < size
    ListNodePosi<T> p = first(); //从首节点出发
    while ( 0 < r-- ) p = p->succ; //顺数第r个节点即是
    return p->data; //目标节点，返回其中所存元素
 }

### 3.3.4 查找

实现
1
2
3
4
5
6

 template <typename T> //在无序列表内节点p（可能是trailer）的n个（真）前驱中，找到等于e的最后者
 ListNodePosi<T> List<T>::find ( T const& e, int n, ListNodePosi<T> p ) const {
    while ( 0 < n-- ) //（0 <= n <= rank(p) < _size）对于p的最近的n个前驱，从右向左
       if ( e == ( p = p->pred )->data ) return p; //逐个比对，直至命中或范围越界
    return NULL; //p越出左边界意味着区间内不含e，查找失败
 } //失败时，返回NULL

### 3.3.5 插入

实现
1
2
3
4
5
6
7
8
9
10
11

 template <typename T> ListNodePosi<T> List<T>::insertAsFirst ( T const& e )
 {  _size++; return header->insertAsSucc ( e );  } //e当作首节点插入
 
 template <typename T> ListNodePosi<T> List<T>::insertAsLast ( T const& e )
 {  _size++; return trailer->insertAsPred ( e );  } //e当作末节点插入
 
 template <typename T> ListNodePosi<T> List<T>::insert ( ListNodePosi<T> p, T const& e )
 {  _size++; return p->insertAsSucc ( e );  } //e当作p的后继插入
 
 template <typename T> ListNodePosi<T> List<T>::insert ( T const& e, ListNodePosi<T> p )
 {  _size++; return p->insertAsPred ( e );  } //e当作p的前驱插入

将新元素e作为当前节点的前驱插至列表的过程

1
2
3
4
5
6

 template <typename T> //将e紧靠当前节点之前插入于当前节点所属列表（设有哨兵头节点header）
 ListNodePosi<T> ListNode<T>::insertAsPred ( T const& e ) {
    ListNodePosi<T> x = new ListNode ( e, pred, this ); //创建新节点
    pred->succ = x; pred = x; //设置正向链接
    return x; //返回新节点的位置
 }

后插入

1
2
3
4
5
6

 template <typename T> //将e紧随当前节点之后插入于当前节点所属列表（设有哨兵尾节点trailer）
 ListNodePosi<T> ListNode<T>::insertAsSucc ( T const& e ) {
    ListNodePosi<T> x = new ListNode ( e, this, succ ); //创建新节点
    succ->pred = x; succ = x; //设置逆向链接
    return x; //返回新节点的位置
 }

3.3.6 基于复制的构造

copyNodes() 
1
2
3
4
5

 template <typename T> //列表内部方法：复制列表中自位置p起的n项
 void List<T>::copyNodes ( ListNodePosi<T> p, int n ) { //p合法，且至少有n-1个真后继节点
    init(); //创建头、尾哨兵节点并做初始化
    while ( n-- ) { insertAsLast ( p->data ); p = p->succ; } //将起自p的n项依次作为末节点插入
 }

3.3.7 删除

1
2
3
4
5
6
7
8
9

template <typename T> T List<T>:: remove(ListNodePPosi(T) p)
{
   T e = p-data;//备份待删除的节点数值
   p->pred->succ= p->succ;
   p->succ->pred = p->pred;//
   delete p;
   _size--;
   return e;//返回备份的数值
}

3.3.8 析构

释放资源，清除节点

1
2
3
4
5
6

template <typename T> List<T>::~List()
{
   clear();
   delete header;
   delete trailer;
   }

3.3.9 唯一化

1
2
3
4
5
6
7
8

 template <typename T> int List<T>::deduplicate() {
    int oldSize = _size; ListNodePosi<T> p = first();
    for ( Rank r = 0; p != trailer; p = p->succ ) //O(n)
       if ( ListNodePosi<T> q = find(p->data, r, p) )
          remove(q); //此时q与p雷同，但删除前者更为简明
       else r++; //r为无重前缀的长度
    return oldSize - _size; //删除元素总数
 }

总体执行时间为 $ O(n^2) $

3.3.10 遍历

实现
1
2
3
4
5
6

 template <typename T> void List<T>::traverse ( void ( *visit ) ( T& ) ) //借助函数指针机制遍历
 {  for ( ListNodePosi<T> p = header->succ; p != trailer; p = p->succ ) visit ( p->data );  }
 
 template <typename T> template <typename VST> //元素类型、操作器
 void List<T>::traverse ( VST& visit ) //借助函数对象机制遍历
 {  for ( ListNodePosi<T> p = header->succ; p != trailer; p = p->succ ) visit ( p->data );  }

3.4 有序列表

3.4.1 唯一化

位置指针p和q分别指向每一对相邻的节点，若两者相同则删除q。

3.4.2 查找

顺序查找，尽管有序列表在逻辑上单调排列，但是在动态存储策略中，节点物理地址与逻辑次序毫无关系。复杂度，O(n)

3.5 排序器

3.5.1 统一入口

插入排序，选择排序，归并排序

3.5.2 插入排序

构思

插入排序(insertionsort)适用于包括向量与列表在内的任何序列结构 思路简述为 始终将整个序列视作并切分为两部分：有序的前缀、无序的后缀 通过迭代，反复地将后缀的首元素转移至前缀中

在任何时刻，相对于当前节点e = S[r] 前缀S[0,r)总是已有序

前缀S[0, r)已经有序。接下来，借助有序序列的查找算法，可在该前缀中定位到不大于e的最大元素。于是只需将e从无序后缀中取出，并紧邻于查找返回的位置之后插入，即可如图(b)所示，使得有序前缀的范围扩大至S[0, r]。 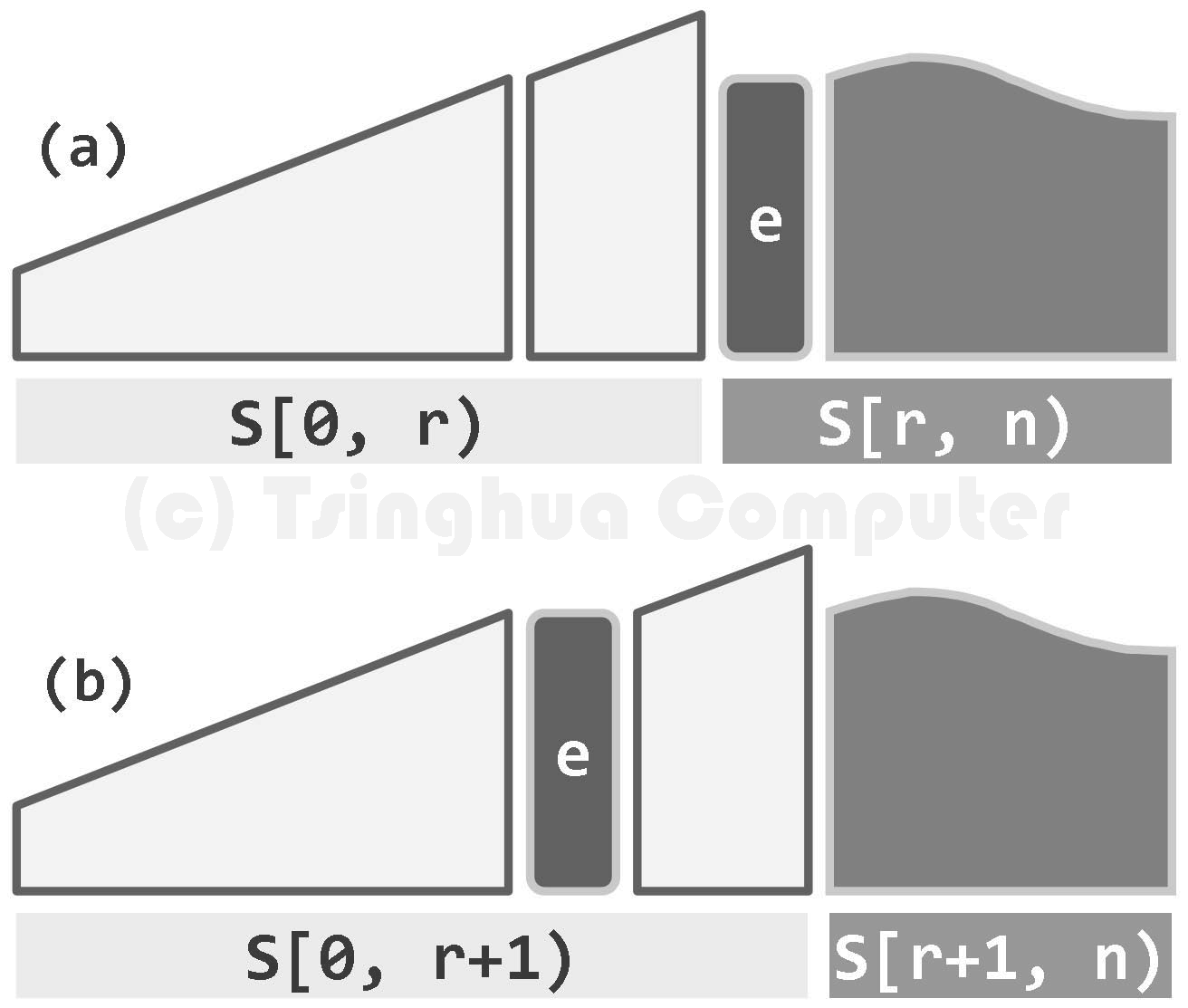复杂度层次

实现

1
2
3
4
5
6
7
8
9
10

template <typename T> // 列表的插入排序算法：对起始于位置p的n个元素排序
void List<T>::insertionSort(ListNodePosi(T) p, int n)
{ // valid(p) && rank(p) + n <= size
    for (int r = 0; r < n; r++)
    {                                                // 逐一为各节点
        insertAfter(search(p->data, r, p), p->data); // 查找适当的位置并插入
        p = p->succ;
        remove(p->pred); // 转向下一节点
    }
}

有多个元素命中时，search()将返回最靠后者。排序之后重复元素将保持原有次序，故以上排序算法属于稳定算法。

复杂度

若输入已经有序式，每次search()操作需要O(1)时间，总体O(n)，若输出完全逆序，则各次search()所需时间线性递增，累计共需O(n^2)时间。

3.5.3 选择排序

与插入排序类似，该算法也将序列划分为无序前缀和有序后缀两部分；此外，还要求前缀不大于后后缀。如此，每次只需从前缀中选出最大者，并作为最小元素转移至后缀中，即可使有序部分的范围不断扩张。

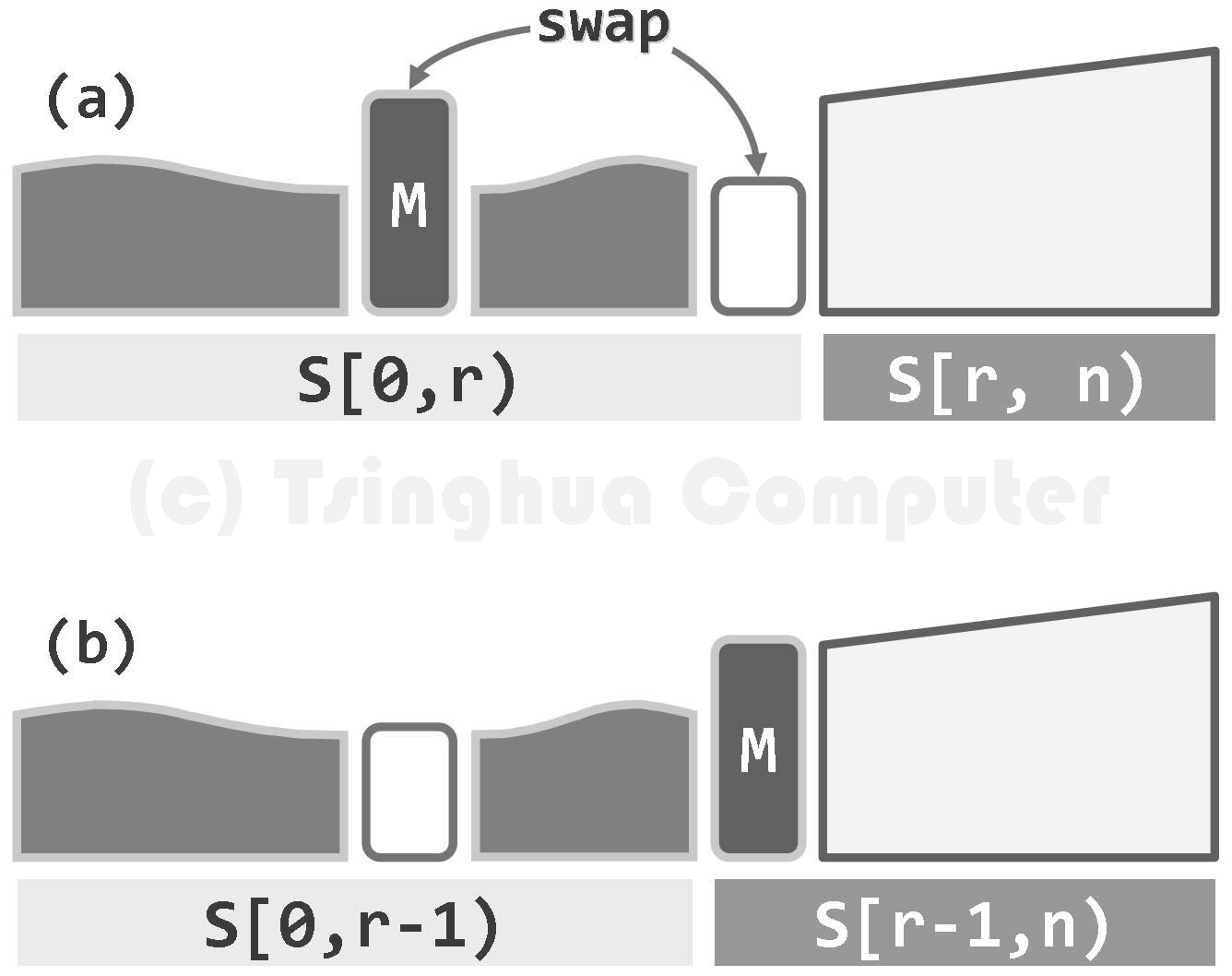
图03-06 序列的选择排序

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

template <typename T> // 列表的选择排序算法：对起始于位置p的n个元素排序
void List<T>::selectionSort(ListNodePosi(T) p, int n)
{ // valid(p) && rank(p) + n <= size
    ListNodePosi(T) head = p->pred;
    ListNodePosi(T) tail = p;
    for (int i = 0; i < n; i++)
        tail = tail->succ; // 待排序区间为(head, tail)//将tail定位到区间末尾
    while (1 < n)
    {                                                   // 在至少还剩两个节点之前，在待排序区间内
        ListNodePosi(T) max = selectMax(head->succ, n); // 找出最大者（歧义时后者优先）
        insertBefore(tail, remove(max));                // 将其移至无序区间末尾（作为有序区间新的首元素）
        tail = tail->pred;
        n--;
    }
}

复杂度

selsectMax()每次必须遍历整个无序前缀，耗时线性正比于前缀长度，累计耗时O(n^2) 选择排序算法时间复杂度固定为O(n^2) 会有很大的改善空间， 借助更高级的数据结构，可以使得单次selectMax()复杂度降低至O(logn)，从而使整体效率提高至O(nlogn)

3.5.4 归并排序

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

template <typename T> // 有序列表的归并：当前列表中自p起的n个元素，与列表L中自q起的m个元素归并
void List<T>::merge(ListNodePosi(T) & p, int n, List<T> &L, ListNodePosi(T) q, int m)
{
    // assert: this.valid(p) && rank(p) + n <= size && this.sorted(p, n)
    // L.valid(q) && rank(q) + m <= L._size && L.sorted(q, m)
    // 注意：在归并排序之类的场合，有可能 this == L && rank(p) + n = rank(q)
    ListNodePosi(T) pp = p->pred;            // 借助前驱（可能是header），以便返回前 ...
    while (0 < m)                            // 在q尚未移出区间之前
        if ((0 < n) && (p->data <= q->data)) // 若p仍在区间内且v(p) <= v(q)，则
        {
            if (q == (p = p->succ))
                break;
            n--;
        }    // 将p替换为其直接后继（等效于将p归入合并的列表）
        else // 若p已超出右界或v(q) < v(p)，则
        {
            insertBefore(p, L.remove((q = q->succ)->pred));
            m--;
        }         // 将q转移至p之前
    p = pp->succ; // 确定归并后区间的（新）起点
}

列表的归并排序算法，可以递归地描述和实现列表的归并排序算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

template <typename T> // 列表的归并排序算法：对起始亍位置p的n个元素排序
void List<T>::mergeSort(ListNodePosi(T) & p, int n)
{ // valid(p) && rank(p) + n <= size
    if (n < 2)
        return;     // 若待排序范围已足够小，则直接迒回；否则...
    int m = n >> 1; // 以中点为界
    ListNodePosi(T) q = p;
    for (int i = 0; i < m; i++)
        q = q->succ; // 均分列表
    mergeSort(p, m);
    mergeSort(q, n - m);          // 对前、后子列表分别排序
    merge(p, m, *this, q, n - m); // 归并
} // 注意：排序后，p依然指向归并后区间的（新）起点

复杂度O(nlogn)

Blogging, Structures and Algorithms
Study
本文由作者按照 CC BY 4.0 进行授权
热门标签
Study PA typography writing
文章内容
热门标签
Study PA typography writing