第四章 栈与队列
栈与队列与列表和向量一样,都是线性序列结构。其基础性是其他结构无法比拟的。
着重介绍如何利用栈结构,实现基于试探回溯策略的高效搜索算法。 在队列方面,将介绍如何实现基于轮值策略的通用循环分配器,并以银行窗口为例实现基础的调度算法
4.1 栈
4.1.1 ADT接口
栈中可以操作的一端更多的称为栈顶,另一方无法操作的称为栈底。
| 操作接口 | 功能 |
|---|---|
| size() | 报告栈的规模 |
| empty() | 判断栈是否为空 |
| push(e) | 将e插至栈顶 |
| pop() | 删除栈顶对象 |
| top() | 引用栈顶对象 |
后出先进
4.1.3 Stack模板类
利用C++继承,按向量模板实现栈结构
1
2
3
4
5
6
7
8
9
#include "../Vector/Vector.h" //以向量为基类,派生出栈模板类
template <typename T>
class Stack : public Vector<T>
{ // 将向量的首/末端作为栈底/顶
public: // size()、empty()以及其它开放接口,均可直接沿用
void push(T const &e) { insert(size(), e); } // 入栈:等效于将新元素作为向量的末元素揑入
T pop() { return remove(size() - 1); } // 出栈:等效亍初除向量的末元素
T &top() { return (*this)[size() - 1]; } // 取顶:直接返回向量的末元素
};
4.2 栈与递归
4.2.1 函数调用栈
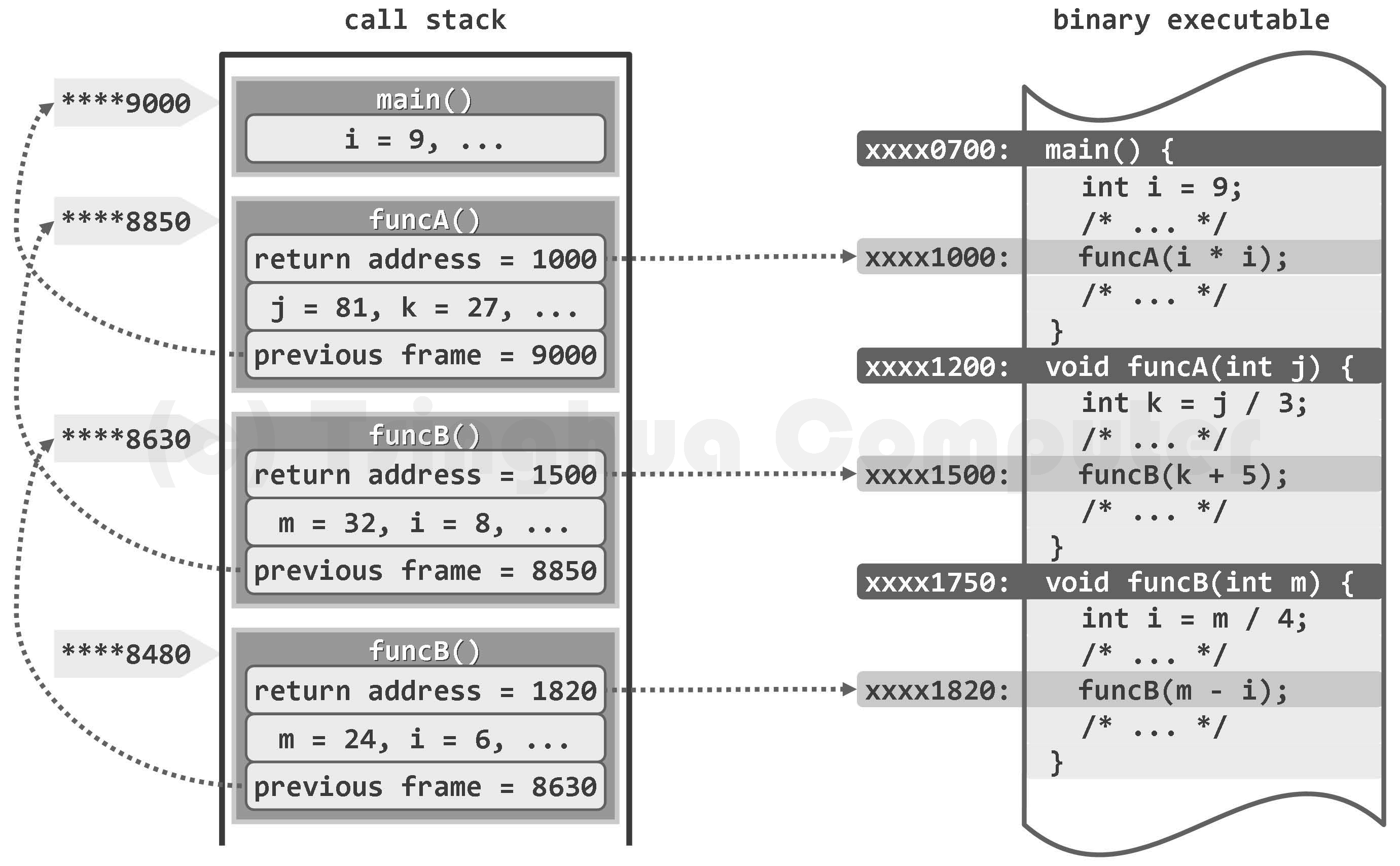
如图4.3所示,调用栈的基本单位是帧(frame)。每次函数调用时,都会相应地创建一帧,记录该函数实例在二进制程序中的返回地址(return address),以及局部变量、传入参数等,并将该帧压入调用栈。若在该函数返回之前又发生新的调用,则同样地要将与新函数对应的一帧压入栈中,成为新的栈顶。函数一旦运行完毕,对应的帧随即弹出,运行控制权将被交还给该函数的上层调用函数,并按照该帧中记录的返回地址确定在二进制程序中继续执行的位置。
在任一时刻,调用栈中的各帧,依次对应于那些尚未返回的调用实例,亦即当时的活跃函数实例(active function instance)。特别地,位于栈底的那帧必然对应于入口主函数main(),若它从调用栈中弹出,则意味着整个程序的运行结束,此后控制权将交还给操作系统。仿照递归跟踪法,程序执行过程出现过的函数实例及其调用关系,也可构成一棵树,称作该程序的运行树。任一时刻的所有活跃函数实例,在调用栈中自底到顶,对应于运行树中从根节点到最新活跃函数实例的一条调用路径。
4.2.2 避免递归
追求高效率的场合,尽量避免递归,尤其是过度的递归
4.3 栈的典型应用
4.3.1 逆序输出
栈所擅长的典型问题中,共同特征:首先,解答以线性序列的形式给出。其次,无论递归还是迭代实现,该序列都是依逆序计算输出的。
进制转换问题
递归式算法
1
2
3
4
5
6
7
8
9
10
11
12
13
void convert(Stack<char> &S, __int64 n, int base)
{ // 十进制n到base进制的转换(迭代版)
static char digit[] // 0 < n, 1 < base <= 16,新进制下的数位符号,可视base取值范围适当扩充。
= {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
while (n > 0)
{ // 由低到高,逐一计算出新进制下的各数位
int remainder = (int)(n % base);
S.push(digit[remainder]); // 余数(当前位)入栈
n /= base; // n更新为其对base的除商
}
} // 新进制下,由高到低的各数位,自顶而下保存到栈中。
4.3.2 递归嵌套
具有自相似性的问题多可以嵌套地递归描述,但因分支位置和嵌套深度并与固定,其递归算法的复杂度与容易控制。 栈结构及其操作天然地具有递归嵌套性。
栈混洗
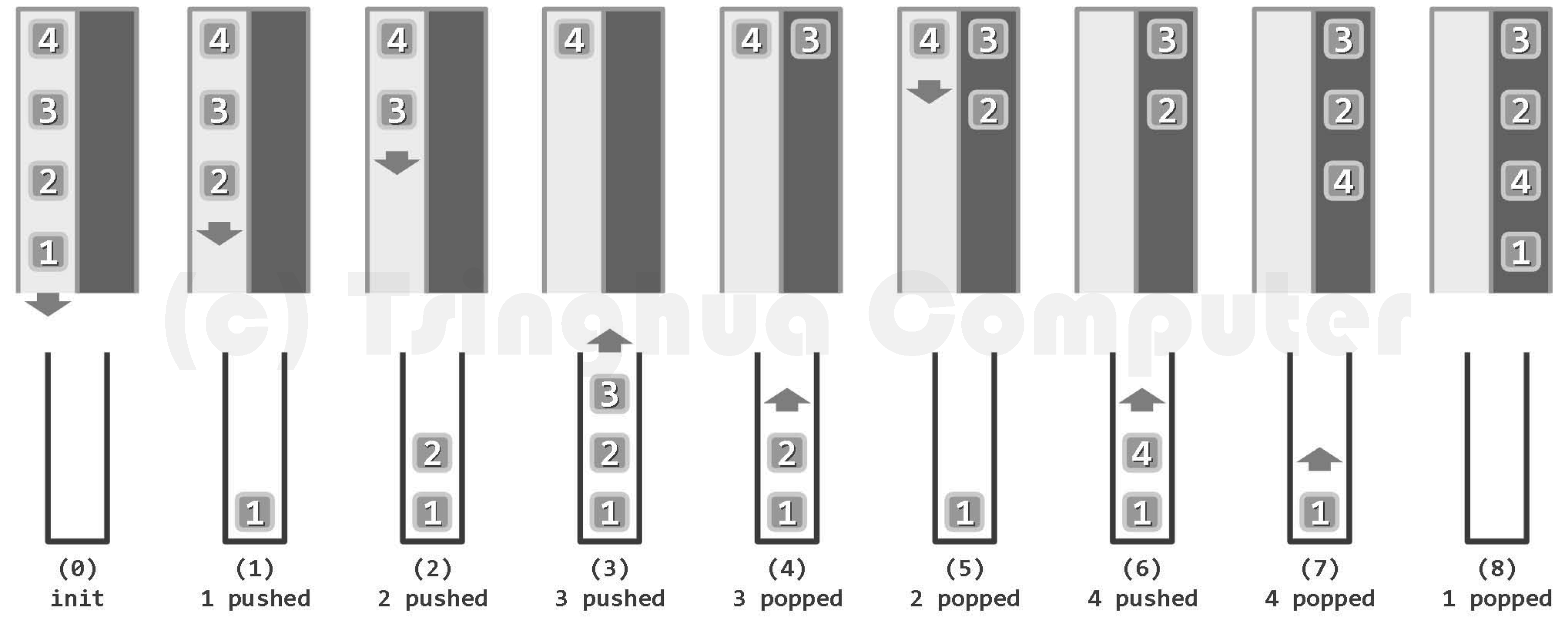
由n次push和n次pop构成的任何操作序列,只要满足“任一前缀中的push与少于pop”这一限制,则该序列也必然对应于某个栈混洗(习题[4-4])。
括号匹配 递归实现
只要将push、pop操作分别与左、右括号相对应,则长度为n的栈混洗,必然与由n对括号组成的合法表达式彼此对应(习题[4-4])。比如,栈混洗{ 3, 2, 4, 1 }对应于表达”( ( ( ) ) ( ) )”。按照这一理解,借助栈结构,只需扫描一趟表达式,即可在线性时间内,判定其中的括号是否匹配。
这一算法可以简明地实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
bool paren(const char exp[], int lo, int hi)
{ // 表达式括号匹配检查,可以兼顾三种括号
Stack<char> S; // 使用栈记录已发现但尚未匹配的左括号
for (int i = 0; exp[i]; i++) /* 逐一检查当前字符 */
switch (exp[i])
{ // 左括号直接进栈;右括号若与栈顶失配,则表达式必与匹配
case '(':
case '[':
case '{':
S.push(exp[i]);
break;
case ')':
if ((S.empty()) || ('(' != S.pop()))
return false;
break;
case ']':
if ((S.empty()) || ('[' != S.pop()))
return false;
break;
case '}':
if ((S.empty()) || ('{' != S.pop()))
return false;
break;
default:
break; // 非括号字符一律忽略
}
return S.empty(); // 整个表达式扫描过后,栈中若仍残留(左)括号,则与匹配;否则栈空(匹配)
}
4.3.3 延迟缓冲
表达式求值
优先级表求值算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
float evaluate(char *S, char *&RPN)
{ // 对(已经删除空白格的)表达式S求值,并转换为逆波兰式RPN
Stack<float> opnd;
Stack<char> optr; // 运算数栈、运算符栈
optr.push('\0'); // 尾哨兵'\0'也作为头哨兵首先入栈
while (!optr.empty())
{ // 在运算符栈非空之前,逐个处理表达式中各字符
if (isdigit(*S))
{ // 若当前字符为操作数,则
readNumber(S, opnd);
append(RPN, opnd.top()); // 读入操作数,并将其接至RPN末尾
}
else // 若当前字符为运算符,则
switch (orderBetween(optr.top(), *S))
{ //视其与栈顶运算符之间优先级高低分别处理
case '<': // 栈顶运算符优先级更低时
optr.push(*S);
S++; // 计算推迟,当前运算符进栈
break;
case '=': // 优先级相等(当前运算符为右括号戒者尾部哨兵'\0')时
optr.pop();
S++; // 脱括号并接收下一个字符
break;
case '>':
{ // 栈顶运算符优先级更高时,可实施相应的计算,并将结果重新入栈
char op = optr.pop();
append(RPN, op); // 栈顶运算符出栈并续接至RPN末尾
if ('!' == op)
{ // 若属于一元运算符
float pOpnd = opnd.pop(); // 叧需叏出一个操作数,并
opnd.push(calcu(op, pOpnd)); // 实施一元计算,结果入栈
}
else
{ // 对于其它(二元)运算符
float pOpnd2 = opnd.pop(), pOpnd1 = opnd.pop(); // 取出后、前操作数
opnd.push(calcu(pOpnd1, op, pOpnd2)); // 实施二元计算,结果入栈
}
break;
}
default:
exit(-1); // 逢语法错误,不做处理直接退出
} // switch
} // while
return opnd.pop(); // 弹出并返回最后的计算结果
}
4.3.4 逆波兰表达式
RPN
逆波兰表达式(RPN)是数学表达式的一种 其语法规则可以概况为:操作符紧邻于对应的(最后一个)操作数之后, 12+ 34^ * 对应于 (1+2) *3 ^4
RPN表达式亦称为后缀表达式,计算效率较高
前一算法在对表达式求值的同时,也顺便完成了从常规表达式到RPN表达式的转换。在求值过程中,该算法借助append()函数=将各操作数和运算符适时地追加至串rpn的末尾,直至得到完整的RPN表达式。 这里采用的规则十分简明:凡遇到操作数,即追加至rpn;而运算符只有在从栈中弹出并执行时,才被追加。这一过程,与上述手工转换的方法完全等效,其正确性也因此得以确立。将RPN自动转换过程与RPN求值过程做一对照,即不难看出,后者只不过是前者的忠实再现。
4.4 试探回溯
4.4.1 试探与回溯
剪枝剪枝,试探。 从零开始,尝试逐步增加候选解的长度。更准确地,这一过程是在成批地考查具有特定前缀的所有候选解。这种从长度上逐步向目标解靠近的尝试,称作试探(probing)。作为解的局部特征,特征前缀在试探的过程中一旦被发现与目标解不合,则收缩到此前一步的长度,然后继续试探下一可能的组合。特征前缀长度缩减的这类操作, 称作回溯 (backtracking),其效果等同于剪枝。如此,只要目标解的确存在就迟早会被发现,而且只要剪枝所依据的特征设计得当,计算的效率就会大大提高。
4.4.2 八皇后
迷宫寻径
4.5 队列
Queue
4.6 队列应用
4.6.1 循环分配器
轮值算法
